
Torricelli formula and its applications
1. Formula - what is Torricelli's theorem
2. Time required to empty a tank / vessel by gravity flow
1. Formula - What is Torricelli's law


Q=Liquid flowrate at orifice (m3/s)
C=Orifice coefficient (-)
A1=Orifice area (m2)
h=Height of liquid from top of tank to middle of orifice (m)
g=gravity acceleration (m.s-2)
g=9.81 m.s-2
C=0.6 for non profiled orifice
Torricelli's law calculation example
A tank has a hole of 10 cm diameter on its side following an incident such as a pipe rupture. The height of liquid above the hole is 5 m. What is the flow of liquid out of the tank ?
STEP 1 : calculate the orifice area
The hole is here circular, thus A1 = π*0.12/4 = 0.0079 m2
STEP 2 : calculate the liquid flowrate
The liquid height above the middle of the hole is 5+0.1/2=5.05 m.
Q = 0.6*0.0079*(2*9.81*5.05)0.5 = 0.047 m3/s = 168 m3/h
2. Time required to empty a tank / vessel by gravity flow
The Torricelli equation can be used to calculate the time required to empty a tank by gravity. Tank emptying time formula :
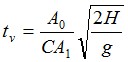
tv=Time in s to discharge a tank up to the level of the
orifice (s)
H=Height of liquid at t=0 (m)
Time to empty a tank calculation example
The tank mentioned in the example in paragraph 2 is considered here. The tank is square, with dimensions of 2m*2m.
STEP 1 : calculate the area A0
The tank is square, this A0 = 2*2 = 4 m2
STEP 2 : calculate the time required to empty the tank
The liquid height above the middle of the hole is 5+0.1/2=5.05 m. A1 has been calculated in the previous example.
tv = 4/(0.6*0.0079)*(2*5.05/9.81)0.5 = 861 s
Source
Mecanique et Rheologie des fluides en genie chimique, Noel Midoux, Lavoisier Tec et Doc, page 51