
Control valves flow characteristics
Control valve flow characteristics and sizing of valves according to the circuit they are in
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
1. Definition of valve flow characteristics
1. Definition of valve flow characteristics
What is the characteristic of a valve ?
- Linear valve
- Exponential valve - also called equal percentage
- Semi quick opening
- Quick opening
Those typical characteristics are shown on the graph below :

2. Usual values
How to size a control valve ?
In order to have a good control, the design of the control valve should be such that it represents around 1/3 of the total pressure drop of the line at maximum flow. The valve must also be designed to work at flows corresponding to 50 to 80 percent of the valve coefficient Cv of the valve fully opened, this is translated by q0 coefficients typically in the range 1.2 to 2.3. Characteristics inside a circuit
How is changing the characteristic of a valve in a circuit ?
One must be very careful when interpreting valve behavior on the field or designing a new installation. Indeed, the characteristics presented above are ideal and not the actual one. Once in the circuit, the characteristic will actually vary depending on the pressure drop through the valve compared to the total pressure drop of the line.
This actually shows that there is only 2 basic types of valve : linear or exponential, with each type that can evolve to one of the standard characteristics when the valve is mounted in series of the circuit - be careful the characteristics is different if the valve is mounted in parallel
4. Linear valve installed in series in a circuit
A linear valve is in the field, once installed on the line, almost
never linear. It will be linear only if the totality of the pressure
drop of the line is created by the valve which is not practically
often true. It must however be noted that, when the valve represent
only few percent of the total pressure drop, the characteristic will
actually be the one of a quick opening valve.

Figure 1 : Change of characteristics of a linear valve as a
function of alpha = pressure drop
through the valve / total pressure drop in the pipe network
considered, at maximum flow.
For the limit condition alpha = 1, which can be considered as the valve alone, we find the linear charactertistic presented above. If one wants to keep a linear characteritics once the valve is in series in a pipe with other element, the pressure drop represented by the valve will have to be at least 2/3 of the total pressure drop, which may not be practical. As mentionned, the practice will be more to have a valve representing around 1/3 of the total pressure drop, which means that its behavior will not be ideal.
5. Exponential valve installed in series in a circuit
An exponential valve will show a behavior of equal percentage only
if it creates the majority of the pressure drop in the line. If it
creates few pressure drop, the characteristics will flatten and
approach a linear characteristics. 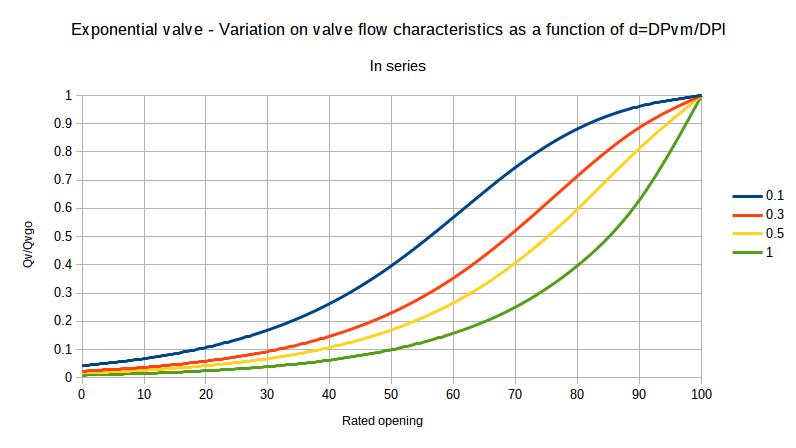
Figure 2 : Change of characteristics of an exponential valve - or
equal percentage - as a function of alpha
= pressure drop through the valve / total pressure drop in the
pipe network considered, at maximum flow.
For the limit condition alpha = 1, which can be considered as the valve alone, we find the exponential charactertistic presented above.
You can access the Excel files having been used to generate the graphs here : Link
6. Control valve gain
Besides the Cv, the other interesting value to know for a control is its gain. The gain is by much the flow (=Cv) will change if the opening of the valve changes. For a control valve, the gain should not be too high around the design valve. For example if the gain in 3, when the valve position is changing by 1% then the flow will change by 3%, which is high and will make the regulation difficult. It is better to target a gain closer to 1 when operating around the design point. The manufacturer should supply a graph showing how the gain changes with the rated opening.
7. Control valve actuator torque
The last characteristic the Engineer should check when selecting a valve is its torque. The torque must be indeed properly sized to ensure a good regulation (undersized actuator may not be strong enough to counter act the pressure of the flow) but also to make sure the valve can close tightly and open easily. The main actuator types have the following torque characteristics :
- Rack and Pinion : The torque will be constant all along the opening
- Pinned crank : The torque will be maximal at around 50% opening
- Scotch yoke : The torque will be maximal when closed and at 100% opening but lowest at around 50% opening
- Articulated crank : The torque is maximal when closed, relatively high at 100% opening.
It is then required to compare the torque charactertistics of the actuator to the torque characteristics of the valve and chose an actuator that is able to deliver higher than the requirement. One order of magnitude is that the valve requirement in the throttling range is representing 40-60% of the actuator max torque in this area [Monsen].
In reality many valves have actually a pinned crank shaft for which the torque is lowest when closing the valve, or when the valve is opened 100%. The sizing of the actuator must then be done on those cases to make sure the valve can close properly, but can also be unseated properly, all the more that many valves actuators are single acting system with a spring used to move the valve in one direction.
8. Nomenclature used in the page
ΔPc=Pressure drop of the circuit - excluding the valveΔPv=Pressure drop of the valve only
ΔPl=total pressure drop of the line, valve + circuit
ΔPcm=Pressure drop of the circuit - excluding the valve - at maximum flow Qvm to be regulated
ΔPvm=Pressure drop of the valve only at maximum flow Qvm to be regulated
d=ΔPvm/ΔPl
Cvgm=Cv of the valve opened for the maximum flow Qvm to be regulated
Cvgo=Cv of the valve full opened
q0=Cvgo/Cvm=margin to make sure the valve is not fully opened at the maximum flow to be regulated, which means the capacity of the valve full open must be higher than the flow to be regulated
Qv=flow through the valve opened at h
Qv0=flow through the valve wide opened
h=relative travel, h=0 when valve closed and h=1 when valve full opened