---

Pump head rise calculation

How to calculate the head rise of a pump ?

Follow us on Twitter
Question, remark ? Contact us at contact@myengineeringtools.com

---

1. Introduction
2. Energy equation : calculation of the head rise through a pump

3. Actual head rise calculation
4. Pump specific work calculation

5. Manufacturers

6. Free Excel calculation tool to calculate head rise

---

1. Introduction

This page is explaining how to calculate the head rise of a fluid when going through a pump.

The head rise through a pump is the difference of head (or energy) that a fluid experience in between the inlet and outlet conditions of a pump. It is important to highlight that the head rise is not only due to the pressure difference, but also to the elevation as well as the velocity.

2. Energy equation : calculation of the head rise through a pump

The head rise - which means the difference of head in between outlet and inlet conditions - can be calculated thanks to the Energy equation of fluids :

H=(P₂-P₁)/(ρ.g)+(h₂-h₁)+(v₂²-v₁²)/2g

With :

H = head rise (m)
P₁ = pressure at inlet conditions considered (Pa)
P₂ = pressure at outlet conditions considered (Pa)
ρ = density of the fluid pumped (kg/m³)
g = gravity acceleration = 9.81 m.s^-2
h₁ = elevation at inlet conditions considered (m)
h₂ = elevation at outlet conditions considered (m)
v₁ = velocity at inlet conditions considered (m)
v₂ = velocity at outlet conditions considered (m)

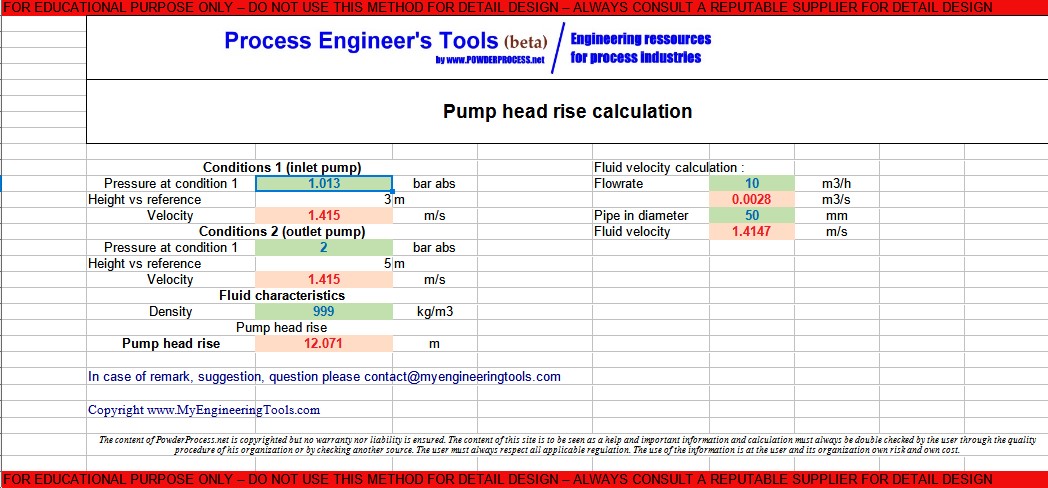
Example

A pump is pumping a liquid from atmospheric conditions to 2 bar abs, the fluid process is water at 25c which has a specific gravity of 999 kg/m3, the flow is 10 m3/h and the pipe diameter is 50 mm. The inlet conditions are the surface of the fluid in a tank at h1 = 3 m and the outlet conditions are in the discharge pipe of pump at h=5 m.

The fluid velocity at condition 1 is 0 m/s, at condition 2 is (10/3600)/(π.0.05²/4)=1.41 m/s

H=(P₂-P₁)/(ρ.g)+(h₂-h₁)+(v₂²-v₁²)/2g=(200000-101325)/(999*9.81)+(5-3)+(1.41²-0²)/(2*9.81) = 12.17 m of water column

Simplification of formula

Note that the example above is given to illustrate the whole equation, however, in most of the cases, the Engineer will be interested in the head rise through the pump, at same inlet / outlet height, and with the same velocity (incompressible fluid, same pipe diameter). The Energy Equation can then be simplified :

H=(P₂-P₁)/(ρ.g)

3. Actual head rise calculation

The formulation above allows to calculate the actual head rise, which means that it is the actual head transferred to the fluid, however, not all the energy from the pump is transferred to the fluid, there are also losses through friction, heat...

H = H_shaft - H_loss

With :

H = actual head (m)
Hshaft = total head as input to the pump shaft (m)
Hloss = losses in the pump

4. Pump specific work calculation

The pump specific work, which means the J input per kg of fluid, can be calculated with the following formula :

W=H.g

With :

W = specific work of the pump in J/kg
H = actual head rise (m)
g = gravity acceleration = 9.81 m.s-2

5. Manufacturers

If you are interested in getting pump characteristics to estimate the head and size of the pump you need for your application, you can contact the pumps GrosClaude : https://www.pompes-grosclaude.com/en/home/

(Note that MyEngineeringTools has no link with this company)

6. Free Excel calculation tool to calculate head rise

You can access an Excel tool to calculate the head rise of a pump thanks to the calculations detailed in this page.

---