
Ideal Gas definition and properties
How to calculate the pressure, volume, density of an ideal gas ?
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
| Section summary |
|---|
| 1. Ideal Gas Law |
| 2. Molar volume of
an ideal gas Vm |
| 3. Mass and volume flow rate correction |
| 4. Volume flow rates corrections |
| 5. Specific heats |
| 6. Ideal Gas Law Excel Calculator |
1. Ideal Gas law
Perfect Gas law / Avogadro Law
Ideal gas assumptions : The ideal gas law allows to represent the behavior of gases at low pressure. In order to reach a simple form, it takes the assumption that there is no interaction in between the molecules of the gas.
Ideal gas formula :
PV = nRT
With
P = absolute pressure of the gas
V = volume of the gas
n = quantity of the gas (in moles)
T = absolute temperature of the gas
R = perfect gas constant
In SI, P is in Pa abs, V is in m3, n is in moles, T is in K and R = 8.314
In US units, P is in PSI abs, V in ft3, n in lbmoles, T is in R, R = 10.73
Note that this expression can also be used with flow rates of gas.
Changes to ideality
The ideal gas law has often be used as a starting point for other equation of states allowing to introduce correction factors to better represent the behavior of gases at higher pressure
2. Molar volume of an ideal gas Vm
The molar volumes of an ideal gas can be calculated from the ideal gas law
PV = nRT
V/n = RT/P
Vm = RT/P
With :
Vm =
molar volume in m3/kmol
T = temperature in K
P = pressure in Pa abs
R = ideal gas constant
The molar volume of an ideal gas in normal conditions is 22.4 l/mol, the normal conditions being T = 0°c, P = 101325 Pa.
3. Mass and volume flow rate conversions
It is possible to convert gas mass to volume flowrate, volume to mass flowrate thanks to the ideal gas law.
Qm = Qv.ρ
Qv = Qm / ρ
Qv = Qm . RT/PM
With :
Qm = mass flowrate in g/h
Qv = volume flowrate in m3/h
M = molecular weight of the gas in g/mol
P = pressure absolute in Pa abs
T = temperature in K
R = 8.314
4. Volume flow rates correction
The volume of a gas in changing depending on the conditions, as gases are compressible. Knowing the volume in condition 1, it is often required to calculate the new volume in condition 2 following a change of pressure or temperature. It is typically what happens along a pipe, where the pressure is changing due to the pressure drop along the pipe and the gas is expanding. If there is no gain or loss of material, the ratio Qv.P/T remains constant.
Qv1.P1/T1 = Qv2.P2/T2
Qv2 = Qv1.T2/T1.P1/P2
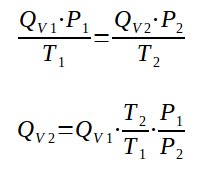
With
Qv1 : volumetric flow rate at condition 1 in m3/h
Qv2 : volumetric flow rate at condition 2 in m3/h
P1 : pressure at condition 1 in Pa
P2 : pressure at condition 2 in Pa
T1 : temperature at condition 1 in K
T2 : temperature at condition 2 in K
Particular case of normal conditions
When performing some calculations with gas, it happens very often that the flow of gas is expressed in Nm3/h, referring to normal conditions. In this case the formula above can be expressed the following way :
Qvn = Qv*273/T*P/1.013
Qv = Qvn*T/273*1.1013/P
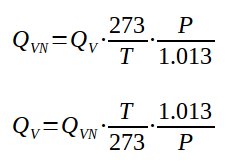
With
Normal conditions : t = 273K and P = 1.013 bar abs
Qvn : volumetric flow rate at normal conditions in Nm3/h
Qv : volumetric flow rate at condition studied in m3/h
P : pressure at condition studied in bar abs
T : temperature at condition studied in K
5. Specific heat of ideal gas
The specific heat at constant pressure of an ideal gas can often be represented through the following form :
Cp = a + bT + cT2 + dT3
The coefficients can be found in tables.
Another specific heat, at constant volume, can be determined for a substance. For an ideal gas, the relations in between the specific heat at constant pressure and at constant volume is given by the following relations :
Cp/Cv = k
If Cp and Cv are in kcal / kmol.K, R = 1.987 kcal/kmol.K :
Cp - Cv = R
k = Cp/(Cp - R)
If Cp and Cv are in kcal / kg.K, R = 8.314 kJ/kmol.K
Cp - Cv = R/M
k =Cp/(Cp - R/M)
k is the isentropic coefficient of ideal gas.
6. Ideal Gas Law Excel Calculator
This ideal gas law calculator will help you calculate the pressure of an ideal gas, the flow of an ideal gas : Ideal Gas Law Calculator
Warning : this calculator is provided to illustrate the concepts mentioned in this webpage, it is not intended for detail design. It is not a commercial product, no guarantee is given on the results. Please consult a reputable designer for all detail design you may need.
