
Shell - Tube Heat Exchanger : transfer coefficient on the tube
side
How to calculate the heat transfer coefficients in the tubes of a shell tube HX ?
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
| Section summary |
|---|
| 1. Heat transfer on
the tube side of a shell tube heat exchanger |
| 2. Calculation of
the heat transfer coefficient on the tube side |
1. Heat transfer on the tube side of a shell tube heat exchanger
The heat exchange in the tubes of a shell heat exchanger depends on the turbulence, i.e. the flow regime, of the fluid. The flow and the physical properties of the fluid are used to calculate the Nusselt number which can be linked to the heat exchange coefficient on the tube side.
The Nusselt number can be expressed as : Nu = h.D/λ
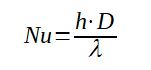
With
Nu = Nusselt number
h = heat transfer coefficient (convection coefficient in the tube)
D = diameter of the tube
λ = thermal conductivity of the fluid
2. Calculation of the heat transfer coefficient on the tube side
How to calculate the heat exchange coefficient inside the tubes of a shell tube heat exchanger ?
2 correlations are proposed here, 1 for laminar flow and the other for turbulent flow.
2.1 Laminar flow (Re < 2100)
The following correlation is from Sieder and Tate
Nu = 1.86.Re1/3.Pr1/3.(di / L)1/3.(μ/μt)0.14

With :
Re = Reynolds number
Pr = Prandtl number = Cp.μ / λ
di = internal diameter of the tube in m
L = length of the tube in m
μ = viscosity of the fluid at bulk temperature in Pa.s (kg/m/s)
μt = viscosity of the fluid a wall temperature in Pa.s
(kg/m/s)
Cp = specific heat of the fluid in J/kg/K (m2/s2/K)
λ = thermal conductivity of the fluid (W/(m.K)) (m⋅kg⋅s−3⋅K−1)
2.2 Turbulent flow (Re > 10000)
The following correlation is from Colburn.
Nu = 0.027.Re0.8.Pr1/3.(μ/μt)0.14

2.3 Calculation of Reynold number
The Reynolds number can be calculated as a function of the mass flow, number of tubes, number of passes, tube diameter.
Re = G.di / μ
G = m / [(Nt/nt).π.di2/4]
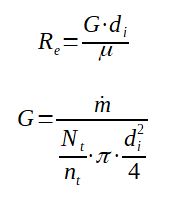
With
G = mass flux in the tube in kg/s/m2
ṁ = mass flow in the heat exchanger on the tube side in kg/s
Nt = number of tubes in the shell tube heat exchanger
nt = number of passes tube in the shell tube heat
exchanger
μ = viscosity of the fluid at bulk temperature in Pa.s (kg/m/s)