Menu

Heat loss from insulated pipe to air

Follow us on Twitter 
Question, remark ? Contact us at contact@myengineeringtools.com

Section summary
1. Heat losses through insulated pipe
2. Example of heat loss calculation of insulated pipe : Step by Step guide
3. Free Excel calculation tool for insulated pipe heat loss : pipe heat loss calculator Excel

In factories, pipes are typically routed outside. This may not be a problem for most of products and circumstances, but in the case of winter conditions or if the product is sensitive to a loss of temperature adding an insulation layer to the pipe is helpful to limit the temperature loss and potential impact on production.



1. Heat losses through insulated pipe

How heat is lost through an insulated pipe ?

There is a heat transfer from the inside of the pipe to the outside air. The heat transfer is a combination of convection and conduction :

  • Convection heat transfer from fluid in pipe to pipe material
  • Conduction through the pipe material
  • Conduction through the insulating material
  • Convection from the insulating material to the outside air

What if your pipe is NOT insulated ?
Consult MyEngineeringTools.com webpage on

Heat loss calculation for non insulated pipes

1.1 Overall heat transfer

The heat transferred from the inside of the pipe to the air can be calculated thanks to the following overall heat transfer equation : Q = U*A*(Ti-Ta)

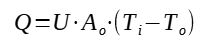
The overall heat transfer coefficient can be calculated by summing  the different resistances to heat transfer the following way :

With :

Q = heat loss (BTU/h)
Ao = heat transfer area (ft2)
U = overall heat transfer coefficient (BTU/h.ft2.F)
Ti = inside temperature (R)
Ta = air temperature (R)
r1 = inside radius of the pipe (ft)
r2 = outside radius of the pipe (ft)
r3 = outside radius of the pipe + insulation layer (ft)
λ1 = thermal conductivity of the pipe (BTU/h.ft.F)
λ2 = thermal conductivity of the insulation (BTU/h.ft.F)
hi = heat transfer coefficient on the inside of the tube (BTU/h.ft2.F)
ho = heat transfer coefficient on the outside of the tube (BTU/h.ft2.F)

1.2 Outside heat transfer coefficient calculation

The heat transfer coefficient has 2 components : one due to radiation heat exchange, and the other due to convection

Radiation heat transfer

In the shortcut calculation method presented in this page, the heat transfer coefficient by radiation is assumed to be hr = 1 BTU/h.ft2.F, as the temperature at the surface of the insulating material is expected to be low.

Convection in the presence of wind

If wind is present, there is a tremendous influence on the heat transfer coefficient which can be estimated the following way : hc = 0.11*c*G0.6/D0.4


Calculation of heat transfer coefficient by convection (with wind)

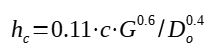
With :

hc = convection heat transfer coefficient (BTU/h.ft2.F)
c = specific heat (BTU/lb/F) = 0.24 for air
G = mass velocity of air (lb/h.ft2) = rho.v
rho = density (lb/ft3) = 0.075 for air
v = wind speed (ft/h)
Do = pipe diameter (ft)

1.3 Total loss of heat through insulated pipe

The overall heat transfer coefficient can be calculated, then the heat loss through the insulation with : Q = U*A*(Ti-Ta)

With U calculated by substituting the heat transfer coefficient calculated above.

2. Example of heat loss calculation of insulated pipe : Step by Step guide

Considering a pipe a 66 mm external diameter and 10 m length that is transporting steam at 160c. What is the heat loss when the pipe is insulated by a 2 cm insulating material, while being located outside, in air at 20c and with wind at 10 km/h.

The pipe is in carbon steel, with a thermal conductivity of 142 W/m.K

The insulating material has a thermal conductivity of 0.086 W/m.K

It is assumed that the skin temperature of the pipe is equal to the temperature of the fluid, the resistance to heat transfer being on the outside of the pipe.

STEP 1 : Convert to US units

Di = 66 mm = 0.2165 ft
Do = 66mm+20*2 = 106 mm = 0.348 ft
L = 10 m = 32.8 ft
Ts = 160c = 320 F = 780 R
Ta = 20c = 68 F = 527.7 R
v = 10 km/h = 32808 ft/h
k1 = 142 W/m.K = 25 BTU/h.ft.F
k2 = 0.086 W/m.K = 0.05 BTU/h.ft.F

STEP 2 : Calculate the heat loss due to radiation

The heat loss due to radiation is expected to be low and estimated to 1 BTU/h.ft2.F

STEP 3 : Calculate the mass velocity of air

Considering G = mass velocity of air (lb/h.ft2) = rho.v

G = rho.v = 0.075*32808 = 2498.8 lb/h.ft2

STEP 4 : Calculate the heat transfer coefficient by convection

The heat transfer coefficient can be calculated from the correlation given in paragraph 1.3 above :

h = 0.11*c*G0.6/Do0.4 =  0.11*0.24*2498.80.6 / 0.3480.4 = 4.4 BTU/h.ft2.F

STEP 5 : Calculate outside heat transfer coefficient

The outside heat transfer coefficient is the sum of  :

ho = hc+hr = 1 + 4.4 = 5.4 BTU/h.ft2.F

STEP 6 : Calculate the overall heat transfer coefficient

U = 1/(0.174/(0.0985*1500) + 0.174*ln(0.10825/0.0985)/25 + 0.174*ln(0.174/0.10825)/0.05 + 1/5.4) = 0.5 BTU/h.ft2.F

STEP 7 : Calculate the total heat loss

Q = U*Ao*(Ts-Ta) =4937.9 BTU/h


3. Free Excel calculation tool for insulated pipe heat loss

The heat flux through a pipe or a pipe with insulation can be calculated thanks to this free pipe heat loss Excel calculator : Calculation Tool - heat loss through insulated pipe (click here)

Warning : this calculator is provided to illustrate the concepts mentioned in this webpage, it is not intended for detail design. It is not a commercial product, no guarantee is given on the results. Please consult a reputable designer for all detail design you may need.

Screenshot Insulated Pipe Heat Transfer calculator

Source

[Chopey] Handbook of Chemical Engineering calculations, Chopey et al, McGraw Hill, 2004