
Plate Heat Exchangers design : Pressure drop calculation
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
| Section summary |
|---|
| 1. Plate heat
exchangers definition |
| 2. Calculation
procedure |
| 3. Plate heat exchanger pressure drop calculator Excel |
1. Pressure drop in plate heat exchanger
How big is the pressure drop in a plate heat exchanger ?
Plate heat exchangers are very efficient equipments to exchange heat. This comes from the fact that the fluid flows in narrow channels in between plates and with a certain degree of turbulence that can be helped through the design of the plate.
This has however a major drawback which is the pressure drop required to "push" the products through these channels and with this level of turbulence. The pressure drop generated by plate heat exchangers is therefore a key design criteria for plate heat exchangers. Before starting the design of an exchanger, the Engineer should know what is the pressure drop that can be afforded in the heat exchanger.
The method presented is simplified and gives an idea of the order of magnitude of pressure drop, it should not be used for detail design and construction of an equipment where the support of a specialized company must be sought.
2. Calculation procedure
How to calculate the pressure drop through a plate heat exchanger ?
The pressure drop in a plate heat exchanger can be estimated thanks to the following correlation :
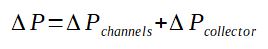
With
ΔP = Pressure drop through the exchanger, per side (Pa)
ΔPchannel = Pressure drop through the exchanger
channels, in between each plate (Pa)
ΔPcollector = Pressure drop in the inlet/outlet ports
of the heat exchanger (Pa)
It has to be calculated on cold and hot side, as the value can be different.
2.1 Calculation of pressure drop in between plates
The pressure drop in a plate heat exchanger can be estimated thanks to the following correlation :

With
ΔPchannel = Pressure drop through the exchanger channels, in between each plate (Pa)f = friction factor (-)
ρ = density of the fluid (kg/m3)
u = velocity of the fluid in between 2 plates (m/s)
Dh = hydraulic diameter = [4*l*dplate] / [2*(l+dplate)] (m)
l = width of the plates (m)
dplate = gap in between 2 plates (m)
L = plate length (m)
The friction factor is calculated according to the following correlations, depending on the Reynolds and on the corrugation of the plates. There is no indication on this site regarding which correlation would be better for a particular case, this needs to be evaluated by the Engineer, you can refer to the references given to know more about the limitations of each correlation.
Some correlations are given below [Neagu] :
Correlation of Mulley which is taking into account the corrugation angle α :

The correlation of Kumar is also quite popular, as a function of the Reynolds [Neagu] :
- f=19.4*Re-0.589 for 10<Re<100
- f=2.990*Re-0.183 for Re>400
Re = Reynolds number (-) = ρ.u.Dh/μ
μ = viscosity of the fluid (Pa.s)
ρ = density of the fluid (kg/m3)
u = velocity of the fluid in between 2 plates (m/s)
Dh = hydraulic diameter = [4*l*dplate] /
[2*(l+dplate)] (m)
l = width of the plates (m)
dplate = gap in between 2 plates (m)
[Kakac] is giving a table of coefficients depending on the angle of corrugation and Reynolds. The friction factor can then be calculated as :
- f=Kp/Rem
With Kp and m from the following table :
| Corrugation angle in ° | Re | Kp | m |
| <30 | <10 | 50 | 1 |
| <30 | 10-100 | 19.4 | 0.589 |
| <30 | >100 | 2.99 | 0.183 |
| 45 | <15 | 47 | 1 |
| 45 | 15-300 | 18.29 | 0.652 |
| 45 | >300 | 1.441 | 0.206 |
| 50 | <20 | 34 | 1 |
| 50 | 20-300 | 11.25 | 0.631 |
| 50 | >300 | 0.772 | 0.161 |
| 60 | <40 | 24 | 1 |
| 60 | 40-400 | 3.24 | 0.457 |
| 60 | >400 | 0.76 | 0.215 |
| >65 | 50 | 24 | 1 |
| >65 | 50-500 | 2.8 | 0.451 |
| >65 | >500 | 0.639 | 0.213 |
2.2 Calculation of pressure drop in the inlet and outlet collectors
It is also necessary to take into account the pressure drop in the manifolds at inlet and outlet (often low compared to the pressure drop inside the exchanger however). [Neagu] is giving the following formula to determine the collectors :

It needs to be calculated on both sides and added to the corresponding main pressure drop.
With (either for cold or hot sides)
ΔPcollector = Pressure drop in the inlet/outlet
ports of the heat exchanger (Pa)
m = mass flow of either cold or hot fluid (kg/s)
Np = number of passes
Dcollector = diameter of the collector on the side
considered (m)
μ = viscosity of the fluid (Pa.s)
ρ = density of the fluid (kg/m3)
3. Plate heat exchanger pressure drop calculator Excel
The plate heat exchanger calculation method given in this page can be applied with a plate heat exchanger calculator Excel, this includes the calculation of the pressure drop of a plate heat exchanger, using the correlations proposed by [Kakac] : calculator
In this tool, the Pr at the wall is assumed to be very close to
the Pr of the bulk fluid (as channels are very narrow), the
correction factor (Pr/Prw) is therefore 1, please make sure it
is a valid assumption in your case.
Warning : this calculator is provided to illustrate the concepts mentioned in this webpage, it is not intended for detail design. It is not a commercial product, no guarantee is given on the results. Please consult a reputable designer for all detail design you may need. Anyone making use of the information above or in the Excel calculator does so at their own risk and assume any and all resulting liability arising therefrom.

[Kakac] Heat Exchangers, Selection, Rating and Thermal Design, Kakac et al, CRC Press