---

Centrifugal compressor : head coefficient, flow coefficient and compression ratio

Follow us on Twitter 
Question, remark ? Contact us at contact@myengineeringtools.com

---

Section summary
1. Performance of an impeller
2. Head coefficient of pressure coefficient
3. Flow coefficient
4. Compression ratio calculation

---

1. Performance of an impeller

It is possible to estimate the performance of a centrifugal compressor, in terms of compression ratio or flowrate if the manufacturer has given some information about the impeller, in addition to basic dimensional data : the head coefficient, the flow coefficient and the polytropic efficiency.

This page aims at answering to the following questions : what is the head coefficient ? What is the flow coefficient ? What is the relation between the head and flow coefficient ? How to calculate the compression ratio given by an impeller ?

2. Head coefficient or pressure coefficient

The head coefficient is an adimensional number that is comparing the polytropic work that one gets during compression to the impeller tip speed

Equation 1 : calculation of compressor head coefficient

With

μ = pressure coefficient
W_p = polytropic work in J/kg
u₂ = tip speed of the impeller in m/s

Order of magnitude of the pressure coefficient :

• Centrifugal flow impeller : 0.5 to 0.6
• Mixed flow impeller : 0.35
• Axial flow impeller : 0.05 to 0.25
• Peripheral flow impeller : 1.8

3. Flow coefficient

The flow coefficient is calculated the following way :

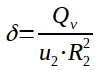
Equation 2 : flow coefficient calculation

With

δ = flow coefficient
u₂ = tip speed of the impeller in m/s
R₂ = impeller outside radius in m
Qv = compressor flowrate in m3/s

Order of magnitude of the flow coefficient :

• Centrifugal flow impeller : 0.04 to 0.2 with until 0.6 for mixed flow
• Axial flow impeller : 0.8 to 1.2
• Peripheral flow impeller : 0.04

Note that there is relation in between μ and δ : the lower the flow coefficient, the higher will be the pressure coefficient. The manufacturer can deliver the curve μ=f(δ) to help size the compressor but one must be careful that the relation will change if the gas handled changed or if the speed of the compressor varies beyond a certain limit

4. Compression ratio calculation

Thanks to the head coefficient it is possible to calculate which compression ratio will be given by an impeller. This calculation is based on the definition of the pressure coefficient and the definition of the polytropic work.

Equation 3 : compression ratio calculation

With

τ = compression ratio
k = isentropic coefficient
μ = pressure coefficient
u₂ = tip speed of the impeller in m/s
M = molar mass of the gas
η_p = polytropic coefficient
R = ideal gas constant
T_suction = suction temperature in K

Note that the compression ratio is actually independent from the suction pressure.

---