
Reaction kinetics : rate laws in batch reactor, single reactant
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
1. Batch reactor : general reaction speed equation
2. Order 0 reaction
3. Order 1 reaction
4. Order 2 reaction
The knowledge of reaction rates is a key data for the design and control of chemical reactors. This page focuses on reaction kinetics in a batch reactor and with a single reactant. It explains how to express and plot the reaction speed for reactions of order 0, 1 and 2.
1. Batch reactor : general reaction speed equation
Assuming that the batch reactor is isotherm, perfectly stirred and of constant volume, the calculation of the mass balance in the reactor shows that the consumption rate of the component A, that is consumed according to the reaction νA = products, is:
r'A = - 1/ν*d[A]/dt
(with ν < 0)
The reaction rate r'A can be expressed as a function of a rate constant k and the concentration of the reactant [A[.
k[A]n = - 1/ν*d[A]/dt
with :
n as the order of reaction
ν as the stoechiometric coefficient
[A] as the concentration in reactant A in the batch reactor at time
t
2. Order 0 reaction
In the case of a reaction of order 0, the reaction rate is independent of the concentration in reactant A, k[A]0 = k
It is then possible to integrate the relation as :
k = - 1/ν*d[A]/dt
k.ν.dt = - d[A]
-[A]+[A]0 = k.ν.(t-t0) = k.ν.t (if t0 = 0)
[A] = [A]0 - k.ν.t
Graphically
It is possible to identify a reaction of order 0 by plotting the
concentration over time. If the graph obtained is a line, the
reaction of is of order 0 and the slope is -k.ν which allows to
calculate the rate constant k if the stoechiometry is known.
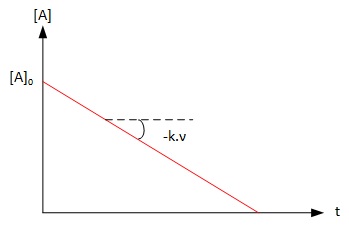
Graph 1 : Graphical identification of a reaction of order 0
Top 5 Most
Popular
1. Compressor
Power Calculation
2. Pump Power Calculation
3. Pipe Pressure
Drop Calculation
4. Fluid Velocity in pipes
5. Churchill Correlation
(friction factor)
3. Order 1 reaction
In the case of a reaction of order 0, the reaction rate is proportional to the concentration in reactant A : k[A] = - 1/ν*d[A]/dt
It is then possible to integrate the relation by rearranging the expression as :
- d[A]/[A] = k.ν.dt
and integrate as :
ln ([A]0/[A]) = k.ν.(t-t0) = k.ν.t (if t0 = 0)
ln ([A]0/[A]) = k.ν.t
Graphically
It is possible to identify a reaction of order 1 by plotting ln ([A]0/[A]) over time. If the graph obtained is a line, the reaction of is of order 1 and the slope is k.ν which allows to calculate the rate constant k if the stoechiometry is known
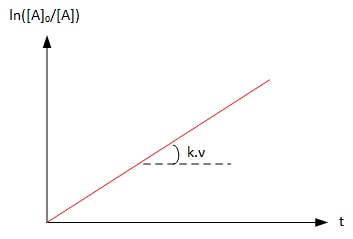
Graph 2 : Graphical identification
of a reaction of order 1
4. Order 2 reaction
In the case of a reaction of order 2, the reaction rate is proportional to the square of concentration in reactant A : k[A]2 = - 1/ν*d[A]/dt
It is then possible to integrate the relation by rearranging the
expression as :
- d[A]/[A]2 = k.ν.dt
and integrate as :
1/[A]-1/[A]0 = k.ν.(t-t0) = k.ν.t (if t0 = 0)
Graphically
It is possible to identify a reaction of order 1 by plotting 1/[A] over time. If the graph obtained is a straight line, the reaction of is of order 2 and the slope is k.ν which allows to calculate the rate constant k if the stoechiometry is known

Graph 3 : Graphical identification of a reaction of order 2