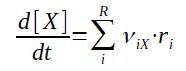Batch Reactors perfectly stirred : mass balance expression
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
1. Batch reactor
2. Batch reactor perfectly stirred and isotherm : mass balance
3. Batch reactor perfectly stirred, isotherm and at constant volume : mass balance
4. Stoechiometry
Batch reactors are quite common in process industries, even if they are not the most performing reactors their simplicity makes it often an attractive choice for small / medium operations. This page focusing in applying the general mass balance equations to batch reactors.
1. Batch reactor
A batch reactor is basically a closed system. The reactants are loaded at the beginning of the process sequence, then the reactor is closed, agitation / heat / cooling is applied, according to the need of the particular process, and the chemical reaction is performed. Once the right conversion rate is reached, the reactor is opened and discharged.
As the reactor is closed during the chemical reaction, there is no entry or exit of materials. The general mass balance equation can then be modified the following way :
Inlet = Outlet + Consumption + Accumulation
0 = 0 + Consumption + Accumulation
The units of each component of the expression is a material flowrate : mol/s for instance.
The different elements in the equation can be expressed the following way :
- Consumption = D'A
- Accumulation = dnA/dt
Which gives the following general expression for a mass balance in a chemical reactor :
0 = 0 + D'A + dnA/dt
Note that the consumption flowrate has a positive sign if the reactant is consumed and a negative sign if the reactant is actually produced.
In the applications below, we consider the case that the batch reactor considered is :
- Perfectly stirred
- Isotherm
2. Batch reactor perfectly stirred and isotherm : mass balance
As the reactor is batch, there is no entry of material and no exit of material, as explained above. The fact to have the reactor perfectly stirred also helps in expressing the consumption / production of reactants and products as it can be expressed as the product of the reaction speed by the volume (r'V)
The mass balance for each component will be the following (r' is a consumption speed and r is a formation speed) :Reactive A
0 = 0 + r'A.V + dnA/dt -> r'A = -1/V * dnA/dt
Reactive B
0 = 0 + r'B.V + dnB/dt -> r'B = -1/V * dnB/dt
Product C
0 = 0 - D'C + dnC/dt -> rC =1/V * dnC/dt
Product D
0 = 0 - D'D + dnD/dt -> rD = 1/V * dnD/dt
Top 5 Most
Popular
1. Compressor
Power Calculation
2. Pump Power Calculation
3. Pipe Pressure
Drop Calculation
4. Fluid Velocity in pipes
5. Churchill Correlation
(friction factor)
3. Batch reactor perfectly stirred, isotherm and at constant volume : mass balance
If the volume is constant over time, the mass balance defined above can be expressed as a function of concentrations (nA/V = [A]) which is particularly helpful during studies as the measurement of concentration is much easier than measuring the total quantity of a component.
Reactive A
r'A = - d[A]/dt
Reactive B
r'B = - d[B]/dt
Product C
rC =d[C]/dt
Product D
rD = d[C]/dt
There is therefore a direct relation in between the reaction
speed and the evolution of the concentration of a reactant or
product over time. This is particularly helpful to measure the
reaction speed during kinetic studies.
4. Stoechiometry
In case the stoechiometry is known, it is possible to find a relation in between the different reaction speeds defined above. The reaction speed becomes then :
rX = 1/ν*d[X]/dt
With :
rX : reaction speed of component X
ν : stoechiometric coefficient of component X (negative if it is a
reactant, positive if it is a product)
[X] : concentration of component X
It is then possible to sum the reaction speed of different reactions where component X is either a reactant or a product of the reaction.
With :
riX : reaction speed of
component X in the reaction i
νiX : stoechiometric coefficient of component X in the
reaction i (negative if it is a reactant, positive if it is a
product)
[X] : concentration of component X
R : number of reactions where X is involved
It is then possible to have a system of equation that can be solved to perform the mass balance and / or perform kinetics studies, as in the example below :
C2H5CHO = C2H6
+ CO
2C2H5CHO = C4H10 + 2CO +
H2
Considering r1 as the speed of the 1st reaction and r2 the speed of reaction 2, the following system of equation can be written on a batch (closed) reactor, perfectly stirred isotherm and with constant volume :
d[C2H5CHO] = -r1 - 2*r2
d[C2H6] = r1
d[C4H10] = r2
d[CO] = r1 + 2*r2
d[H2] = r2