
Mass Balance in reactors : general relations
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
1. Mass balance in a chemical reactor
2. Applying the mass balance equation to a chemical reaction
3. Reaction speed
4. Particular case : Reactor in steady state
5. Particular case : perfectly stirred reactor
A mass balance is the starting point of every study in Chemical Engineering. This page is explaining how to perform a mass balance in a chemical reactor. The general considerations defined here can then be refined when applied to specific situations (closed reactor, steady state...).
1. Mass balance in a chemical reactor
Let's consider a component A that enters a chemical reactor, the component can have different fates depending on what happens in the system :
- It can just leave the system in the same state it entered
- It can disappear, or appear, for example through a chemical reaction
- It can stay in the reactor, what we will call accumulate in the reactor
Those different quantities, when summed, should be equal to the amount of material introduced in the reactor (nothing has disappeared, all material entered must have gone somewhere !). The following general mass balance relation can therefore be written :
Inlet = Outlet + Consumption + Accumulation
The units of each component of the expression is a material flowrate : mol/s for instance.
The different elements in the equation can be expressed the following way :
- Inlet = FA,i
- Outlet = FA,o
- Consumption = D'A
- Accumulation = dnA/dt
Which gives the following general expression for a mass balance in a chemical reactor :
FA,i = FA,o + D'A + dnA/dt
Note that the consumption flowrate has a positive sign if the reactant is consumed and a negative sign if the reactant is actually produced.
2. Applying the mass balance equation to a chemical reaction
Considering a chemical reaction whose stoechiometry is not known : A + B = C + D, the mass balance for each component will be the following :
Reactive A
FA,i = FA,o + D'A + dnA/dt
Reactive B
FB,i = FB,o + D'B + dnB/dt
Product C
0 = FC,o - D'C + dnC/dt (there is no product C at the inlet of the reactor, and the chemical reaction is creating C, not consuming it, which changes the sign in front of the consumption term) -> D'C = FC,o + dnC/dt
Product D
0 = FD,o - D'D + dnD/dt (there is no product D at the inlet of the reactor, and the chemical reaction is creating D, not consuming it, which changes the sign in front of the consumption term) -> D'D = FD,o + dnD/dt
3. Reaction speed
The consumption term D' given above is actually the reaction speed
r' integrated over the whole volume of reactants. The reaction speed
of the reactant A may vary within the reactor due to concentration
of materials, pressure, temperature, thus it should be calculated as
integral over the entire volume :
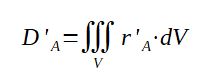
With :
D'A = consumption speed of reactant A (mol/s)
r'A = reaction speed of A (mol/s/m3)
dV = unit of volume (m3)
Top 5 Most
Popular
1. Compressor
Power Calculation
2. Pump Power Calculation
3. Pipe Pressure
Drop Calculation
4. Fluid Velocity in pipes
5. Churchill Correlation
(friction factor)
4. Particular case : Reactor in steady state
It happens often that a reactor is operated in steady state : this means that there is no accumulation in the reactor. No accumulation means that the concentration is not varying over time, thus the term dn/dt is equal to 0. Considering the reaction above.
Steady state - > dnA/dt = dnB/dt = dnC/dt = dnD/dt = 0
The mass balance for each component will be the following :
Reactive A
FA,i = FA,o + D'A
Reactive B
FB,i = FB,o + D'B
Product C
0 = FC,o - D'C + dnC/dt (there is no product C at the inlet of the reactor, and the chemical reaction is creating C, not consuming it, which changes the sign in front of the consumption term) -> D'C = FC,o
Product D
0 = FD,o - D'D + dnD/dt (there is no product D at the inlet of the reactor, and the chemical reaction is creating D, not consuming it, which changes the sign in front of the consumption term) -> D'D = FD,o
This can be particularly interesting for kinetic studies as the formation of C and D is equal to the consumption (production in this case) rate.
5. Particular case : perfectly stirred reactor
If the reactor is perfectly agitated, it means that the concentration in the reactor is equal at any point of the reactor. In this case, the triple integral can be simplified as the concentration is equal in each dV. The consumption speed is just r'.V
The mass balance for each component will be the following :
Reactive A
FA,i = FA,o + r'A.V + dnA/dt
Reactive B
FB,i = FB,o + r'B.V + dnB/dt
Product C
0 = FC,o - D'C + dnC/dt (there is no product C at the inlet of the reactor, and the chemical reaction is creating C, not consuming it, which changes the sign in front of the consumption term) -> r'C.V = FC,o + dnC/dt
Product D
0 = FD,o - D'D + dnD/dt (there is no product D at the inlet of the reactor, and the chemical reaction is creating D, not consuming it, which changes the sign in front of the consumption term) -> r'D.V = FD,o + dnD/dtWhen combined to an operation in steady state (see above) a perfectly stirred reactor can also help a lot kinetic studies.